Complex Numbers

Definitions

The imaginary unit $i$ is defined as $i = \sqrt{-1}$. In other words $i^2 = -1$.

Imaginary numbers are of the form $bi$, where $b$ is a real number and $i$ is the imaginary unit. Complex numbers are linear combinations of real and imaginary numbers.

Standard form for Complex numbers

$$z = a + ib,$$

where $a$ and $b$ are real numbers.

The real part of $z$ is $\text{Re}(z) = a$ and the imaginary part of $z$ is $\text{Im}(z) = b$ (see Figure 1).

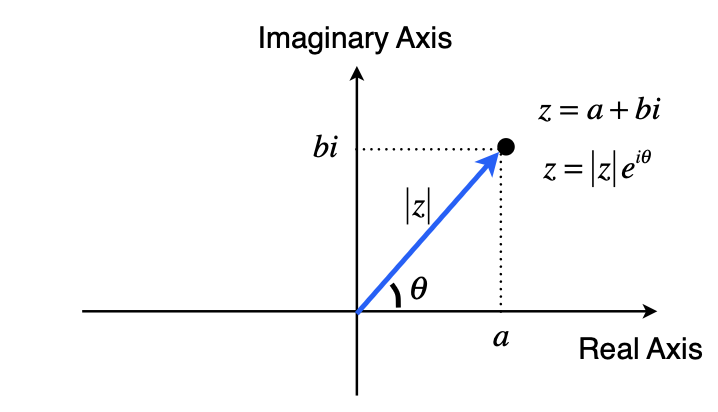
Figure 1: Complex plane with real and imaginary axes..

The complex conjugate of $z$ is defined as

z^* \equiv a - bi.

The complex conjugate may be thought of as a reflection across the real axis in the complex plane (see Figure 2). It is simple to show that the complex conjugate of any complex number may be found by simply replacing $i$ with $-i$ even in more complicated expressions where $i$ appears multiple times, in the denominator, etc.

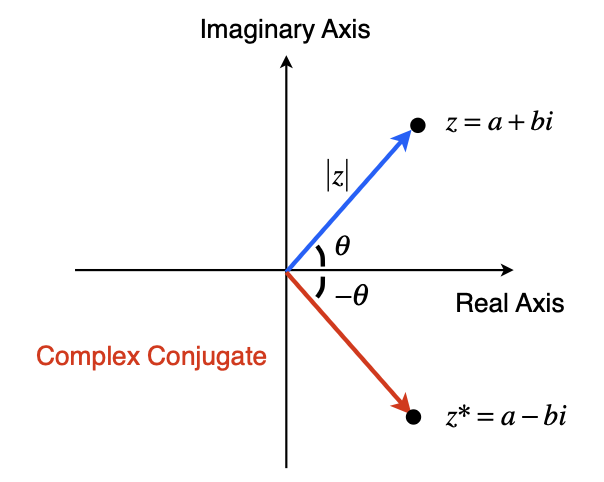
Figure 2: Complex conjugate $z^*$ in the complex plane..

Modulus:

The modulus $|z|$ of a complex number $z$ is defined as the distance from the origin to the point in the complex plane. The square of the modulus is equal to the product of the complex number and its conjugate:

\begin{align*} |z|^2 &= z^* z \\ &= a^2 + b^2. \end{align*}

Proof. We can write $z$ as $z = a + bi$ and $z^* = a - bi$. After cross-multiplying, and substituting $i^2 = -1$, we get:

\begin{align*} |z|^2 &= z^* z \\ &= (a-bi)(a+bi)\\ &= a^2 + bi - bi -(i)^2b^2 \\ &= a^2 + b^2. \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;✅ \end{align*}

Polar Form

If we introduce $\theta$ as the angle from the real axis to the point defined by $z$, then we can interpret $|z| \cos \theta$ as the projection of $z$ onto the real axis and $|z| \sin \theta$ as the projection of $z$ onto the imaginary axis (see Figure 1).

\begin{align*} Re(z) &= a = |z| \cos \theta \\ Im(z) &= b = |z| \sin \theta \\ \end{align*}

We can now write our complex number $z$ in terms of polar coordinates $\theta$ and $|z|$:

\begin{align*} z &= a + bi \\ &= |z| \cos \theta + i |z| \sin \theta \\ &= |z| (\cos \theta + i \sin \theta) \end{align*}

We'll need to introduce Euler's formula in the next section before we arrive at our final, most compact way of writing a complex number $z$ in terms of polar coordinates.

Euler's Formula

Euler's formula gives us an elegantly compact way to write the the polar form of complex numbers $z$ using the exponential function:

Euler's Formula

e^{i \theta} = \cos \theta + i \sin \theta

This formula is a direct consequence of the Taylor series expansions of the exponential function and the sine and cosine functions.

We can now use Euler's formula to write our complex number $z$ in terms of polar coordinates:

\begin{align*} z &= a + bi \\ &= |z| (\cos \theta + i \sin \theta) \\ &= |z| e^{i \theta}. \end{align*}

Polar Form of a Complex Number

\begin{align*} z &= |z| e^{i \theta} \\ &= |z| (\cos \theta + i \sin \theta) \end{align*}

Notice that this result tells us that whenever we see a complex exponential $e^{i \theta}$, we can think of the value multiplying the imaginary unit $i$ ($\theta$ in this case) as an angle in the complex plane.

The real and imaginary parts of the complex exponential $z = |z| e^{i \theta}$ are shown in Figure 3.

\begin{align*} \text{Re}( |z| e^{i \theta}) &= |z| \cos \theta \\ \text{Im}( |z| e^{i \theta}) &= |z| \sin \theta \\ \end{align*}

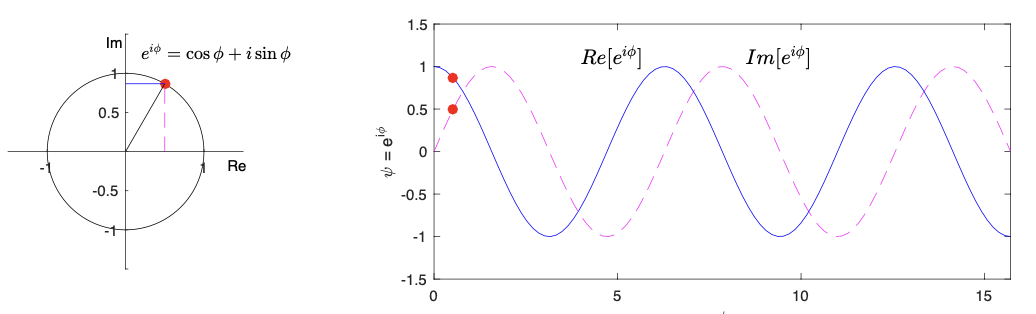
Figure 3: Real and imaginary parts of the complex exponential $z = |z| e^{i \theta}$..

Example: Find the complex conjugate of the polar form of a complex number, $z = |z| e^{i \theta}$.

Solution:

The simple way to find the complex conjugate of a complex number is to simply replace each instance of $i$ with $-i$:

\begin{align*} z^* &= \left[|z| e^{i \theta}\right]^* \\ &= |z| e^{-i \theta} \;\;\;\;\;\;\; ✅\\ \end{align*}

We can verify this result by writing it in standard form:

\begin{align*} z^* &= |z| e^{-i \theta} \\ &= |z| (\cos (-\theta) + i \sin (-\theta)) \\ &= |z| \cos \theta - i |z|\sin \theta . \end{align*}

This result is the complex conjugute of the original complex number $z=|z|(\cos \theta + i \sin \theta)$.

Unit Circle

The unit circle in the complex plane may be defined as all complex numbers with modulus one, $|z| = 1$. Thus,

\begin{align*} z_\text{unit} &= e^{i\theta} \\ &= \cos \theta + i \sin \theta . \end{align*}

Let's plug in some values for $\theta$ to see what we get:

Special Points on the Unit Circle:

\begin{align*} e^{i0} & = \cos (0) + i \sin (0) = 1\\ e^{i\pi/2} & = \cos (\pi/2) + i \sin (\pi/2) = i\\ e^{i\pi} & = \cos (\pi) + i \sin (\pi) = -1\\ e^{i3\pi/2} & = \cos (3\pi/2) + i \sin (3\pi/2) = -i. \end{align*}

We can plot these points on the unit circle in the complex plane (see Figure 4):

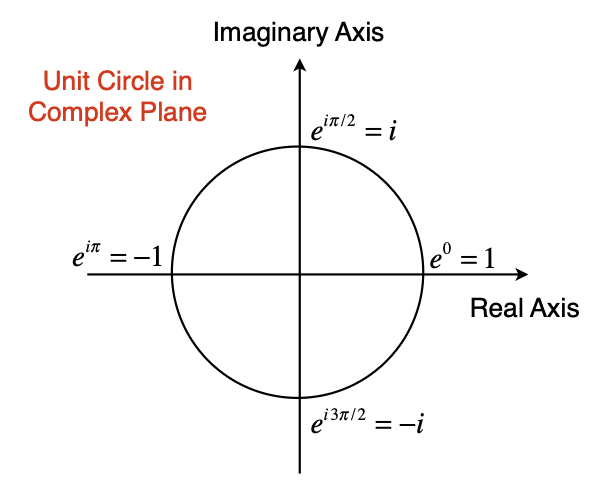
Figure 4: Unit circle in the complex plane.

Operations with Complex Numbers

Addition and Subtraction

Addition of complex numbers is very similar to the addition of vectors. We simply add the real and imaginary parts independently. For example, if we have two complex numbers $z_1 = a_1 + i b_1$ and $z_2 = a_2 + i b_2$, then their sum is given by:

\begin{align*} z_1 + z_2 &= \left( a_1 + i b_1\right) + \left( a_2 + i b_2\right) \\ &= \left( a_1 + a_2\right) + i \left( b_1 + b_2\right) . \end{align*}

It is almost always easier to add complex numbers in their rectangular form $a + ib$ rather than in their polar form $e^{i \theta}$.

Subtraction of complex numbers is similar to addition. We simply subtract the real and imaginary parts independently.

\begin{align*} z_1 - z_2 &= \left( a_1 + i b_1\right) - \left( a_2 + i b_2\right) \\ &= \left( a_1 - a_2\right) + i \left( b_1 - b_2\right) . \end{align*}

Multiplication and Division

When multiplying two complex numbers, we can either use the rectangular $a+bi$ form or the polar $|z|e^{i \theta}$ form.

In the standard form, we "foil it out" and and group the real and imaginary terms:

\begin{align*} z_1 z_2 &= \left( a_1 + i b_1\right) \left( a_2 + i b_2\right) \\ &= \left( a_1 a_2 - b_1 b_2\right) + i \left( a_1 b_2 + a_2 b_1\right) . \end{align*}

While this is a straightforward process, it does not give us a very intuitive picture of what is happening.

Example: Multiply the complex numbers $z_1 = 2 + 3i$ and $z_2 = 4 + 5i$.

\begin{align*} z_1 z_2 &= (2 + 3i) (4 + 5i) \\ &= 8 + 10i + 12i + 15i^2 \\ &= 8 + 22i - 15 \\ &= -7 + 22i. \end{align*}

Let's now multiply complex numbers in polar form. Given two complex numbers $z_1 = |z_1| e^{i \theta_1}$ and $z_2 = |z_2| e^{i \theta_2}$, their product is given by:

\begin{align*} z_1 z_2 &= |z_1| e^{i \theta_1} |z_2| e^{i \theta_2} \\ &= |z_1| |z_2| e^{i (\theta_1 + \theta_2)} . \end{align*}

This result is much more intuitive than the standard form. It tells us that the modulus of the resultant complex number is the product of the moduli of the original numbers and the angle is the sum of the angles of the original numbers.

Example: Multiply the complex numbers $z_1 = 3 e^{i \pi/2}$ and $z_2 = 2 e^{i \pi/4}$.

\begin{align*} z_1 z_2 &= (3 e^{i \pi/2}) (2 e^{i \pi/4}) \\ &= 6 e^{i (\pi/2 + \pi/4)} \\ &= 6 e^{i 3\pi/4}. \end{align*}

Notice that the modulus of the resultant complex number is the product of the moduli of the original numbers ($3 \times 2 = 6$) and the angle is the sum of the angles of the original numbers ($\pi/2 + \pi/4 = 3\pi/4$).

Interactive Complex Number Multiplication

This visualization shows how two complex numbers multiply in the complex plane. The product $z_1 \cdot z_2$ has a modulus equal to the product of the moduli and an angle equal to the sum of the angles.

Result: Modulus: 1.0 | Angle: 0.0 rad

Division of complex numbers is similar to multiplication. We simply divide the modulus of the two numbers and subtract the angle of the second number from the angle of the first number: Given two complex numbers $z_1 = |z_1| e^{i \theta_1}$ and $z_2 = |z_2| e^{i \theta_2}$, their quotient is given by:

\begin{align*} \frac{z_1}{z_2} &= \frac{|z_1| e^{i \theta_1}}{|z_2| e^{i \theta_2}} \\ &= \frac{|z_1|}{|z_2|} e^{i (\theta_1 - \theta_2)} . \end{align*}

Multiplication by $e^{\pm i \phi}$

Let's see what happens when we multiply a complex number $z=|z| e^{i\theta}$ by $e^{i \phi}$:

\begin{aligned} z e^{i \phi} &= |z| e^{i\theta} \cdot e^{i \phi} \\ &= |z| e^{i(\theta + \phi).} \end{aligned}

We see that the resultant complex number simply rotates in the complex plane by an angle $\phi$ without changing its "length" $|z|$:

Similarly, multiplying by $e^{-i \phi}$ is equivalent to a rotation by $-\phi$ radians in the complex plane.

\begin{align*} z e^{-i \phi} &= |z| e^{i\theta} \cdot e^{-i \phi} \\ &= |z| e^{i(\theta - \phi)} . \end{align*}

Negation

The negative of a complex number may be found by negating both the real and imaginary components

$$-z = -a - ib$$

We can also substitute $e^{i\pi} = -1$ into the expression for $-z$ to get:

\begin{aligned} -z &= (-1) z \\ &= \left( e^{i\pi} \right) \left( |z| e^{i\theta} \right) \\ &= |z| e^{i(\theta + \pi)} \end{aligned}

Thus, negation may be seen as a rotation by $\pi$ radians in the complex plane.

Simplifying Complex Numbers

When a complex number is in the denominator of a fraction, we can simplify the expression by multiplying by the numerator and denominator by the complex conjugate of the denominator.

Example: Write the expression $\frac{1}{1+i}$ in standard form.

Solution:

We can simplify the expression by multiplying by the numerator and denominator by the complex conjugate of the denominator:

\begin{align*} \frac{1}{1+i} &= \frac{1}{1+i} \left( \frac{1-i}{1-i} \right) \\ &= \frac{1-i}{(1+i)(1-i)} \\ &= \frac{1-i}{1-i^2} \\ &= \frac{1-i}{1-(-1)} \\ &= \frac{1-i}{2} \\ &= \frac{1}{2} - \frac{i}{2}. \end{align*}

This result is the simplified expression of the original complex number $z=1/(1+i)$.

Some Useful Complex Exponential Identities

\begin{align*} e^{i\phi} &= \cos \phi + i \sin \phi\\ e^{-i\phi} &= \cos \phi - i \sin \phi\\ \cos \phi &= \frac{e^{i\phi} + e^{-i\phi}}{2} \\ \sin \phi &= \frac{e^{i\phi} - e^{-i\phi}}{2i} \end{align*}